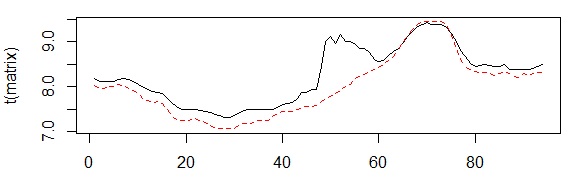
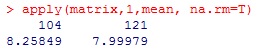
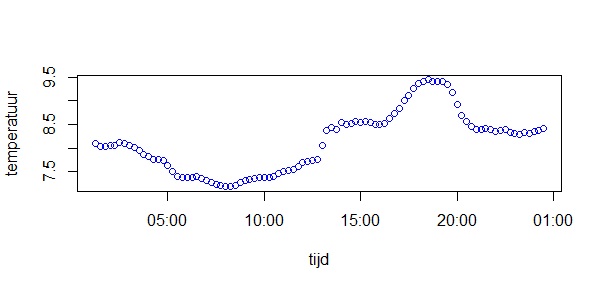
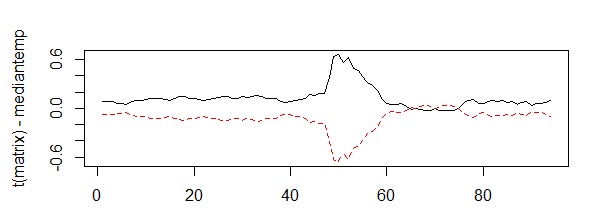
Analyse meetkastjes data

Haal de data op
Zet de tijden goed, want ze zenden niet allemaal tegelijk hun data door
Doe de analyses

Haal de data van meerdere meetkastjes op

# maak een variabele genaamd 'start', met het beginmoment van je grafiek
start<-"2017-10-20,00:00"

# maak een variabele genaamd 'eind', met het eindmoment van je grafiek
end<-"2018-01-15,23:59"

# maak variabele 'ids', met het nummer van de sensor die je wilt bekijken
# voorbeelden: "13", "13,14", "1-50", "1,2,10-20", etc.
ids<-"1-50"
ids<-"121,104"
ids<-"11,14,19,26,31,37,41,47" (windroos)
ids<-"67,60,74,22,10" (centrum, west, zuid, noord, oost)

# haal de data op van de server van Meet je Stad
data<-read.table(paste("http://meetjestad.net/data?
type=sensors&start=",start,"&end=",end,"&ids=",ids,"&format=csv", sep=""), sep="\t", header=T, fill=T)

# op de server zijn alle metingen opgeslagen in Universal Time Code. Laten we deze globale tijd omrekenen naar onze lokale tijd
ts<-as.POSIXct(data$timestamp, origin="1970-01-01", tz="UTC")
data$localtime<-as.POSIXct(ts, "CET")
attributes(data$localtime)$tzone <- "CET"

# zoek de hoogste en de laagste temperatuur van de opgehaalde datareeks
# we gebruiken het 5e en 95e percentiel van de meetwaarden, en trekken daar 1 graad of of tellen het erbij
ylow<-quantile(data$temperature,0.05)-1
yhigh<-quantile(data$temperature,0.95)+1

# maak een grafiek van de data (lijnen)
ggplot(data=data, aes(localtime,temperature, colour = as.factor(id))) +
geom_line(aes(group = as.factor(id)) ) +
ylim(ylow,yhigh)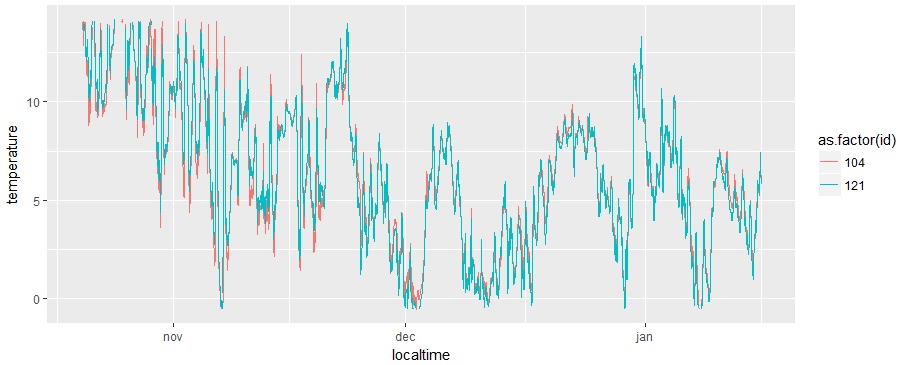

Zet de tijden goed

# Maak een vector met de vroegste en laatste tijd
tsrange <- range(data$localtime)
# rond deze start- en eindtijd af naar het dichtstbijzijnde kwartier
startkwartier<-as.POSIXlt(round(as.double(tsrange[1])/(15*60))*(15*60),origin=(as.POSIXlt('1970-01-01')))
eindkwartier<-as.POSIXlt(round(as.double(tsrange[2])/(15*60))*(15*60),origin=(as.POSIXlt('1970-01-01')))
# maak een reeks van het beginkwartier tot het eindkwartier in stappen van 15 minuten
tssequence <- seq(startkwartier+15*60,eindkwartier-15*60, by=15*60)
# maak een data frame met een lege matrix voor alle stations en kwartieren
matrix<-data.frame(matrix(,nrow=length(levels(factor(data$id))),ncol=length(tssequence) ) )

# vul de matrix
# van iedere reeks metingen van een station,
# berekenen we de lineaire interpolartie naar de kwartier tijden
j<-0
for (i in as.numeric(levels(factor(data$id))) ) {
tree <- subset(data, id==i)
ltime <- tree$localtime
if (length(ltime) > 1) {
j<-j+1
interpol<-approx( as.numeric(ltime),tree$temperature, xout=as.numeric(tssequence), rule=1, method = "linear", ties=mean)
matrix[j,] <- c(interpol$y)
}
}
# geeft de kolommen en rijen namen
colnames(matrix)<-tssequence
rownames(matrix)<-levels(factor(data$id))

ja ja .... (ik doe ook maar kopieren en plakken)

Doe de analyses

Een simpele plot van de (getransponeerde) matrix matplot(t(matrix), type="l")
Bereken de gemiddelde temperatuur per station 1 = rij, 2 = kolom apply(matrix,1,mean, na.rm=T)
Bereken de minima en de maxima apply(matrix,1,max, na.rm=T) apply(matrix,1,min, na.rm=T)
Bereken de gemiddelde temperatuur van alle stations, per kwartier apply(matrix,2,mean, na.rm=T) lange lijst voor elk kwartier plaatje van laatste 4 kwartieren
Plot de modale temperatuur Modaal is het meest voorkomende: median() Het echte gemiddelde is het gemiddelde: mean() mediantemp <- as.numeric(apply(matrix,2,median, na.rm=T)) plot(tssequence, mediantemp,ylab="temperatuur", xlab="tijd", type="b", col="blue") type="b" zowel punten als een lijn
Plot het verschil tov de modale temperatuur matplot(t(matrix)-mediantemp, type="l")
De maximale afwijking van het gemiddelde per station apply(t(matrix)-mediantemp,2,max, na.rm=T)
Plot het verschil tussen 2 stations Zorg dat ze in de data frame zitten! station1<-104 station2<-121 plot(tssequence, as.numeric(matrix[levels(factor(data$id))==station1,] - matrix[levels(factor(data$id))==station2,]), ylab="temperatuur", xlab="tijd", type="b", col="blue")
Zoek de maximale standaard deviatie tussen de stations De standaard deviatie geeft aan hoeveel er gemiddeld afgeweken wordt van het gemiddelde. De standaard deviatie wordt bepaald met de functie sd() max(apply(matrix,2,sd, na.rm=T))
Zoek het tijdstip met de maximale standaard deviatie tussen de stations which.max(apply(matrix,2,sd, na.rm=T))
Plot de standaard deviatie plot(tssequence, apply(matrix,2,sd, na.rm=T), ylab="sd temperatuur", xlab="tijd", type="b", col="blue") Is bij twee stations hetzelfde als het verschil tussen twee stations Deze wordt pas leuk bij meerdere stations
Stations die meer dan 10 graden afwijken! slechtestations <- abs(apply(t(matrix)-mediantemp,2,max, na.rm=T)) > 10 which(slechtestations==T) antwoord 0, deze twee stations wijken niet meer dan 10 graden af
Stations minder dan 10 graden afwijken goedematrix <- matrix[!slechtestations,] matplot(t(goedematrix), type="l")